Почему ракушка наутилус имеет этот странный и элегантный вид?

Начало исследования этой спирали должно быть связано с навигацией. На протяжении XVI и XVII веков тысячи судов бороздили океаны. Мореплаватели знали, что на поверхности Земли кратчайшее расстояние между двумя точками дает дуга окружности. Но чтобы двигаться по такой дуге следует непрерывно менять направление движения.Поэтому этот оптимальный курс заменяли другим, таким, чтобы угол, под которым корабль пересекал все меридианы, был постоянным. Этот курс оставался постоянным. Траектории такого вида образуют на земной поверхности кривые, которые называются локсодромами. Однако моряки не работали на сфере, их карты были плоскими, они представляли собой проекции сферы. Ну а проекция сферы на плоскость преобразует локсодрому на ней в… логарифмическую (или равноугольную) спираль.

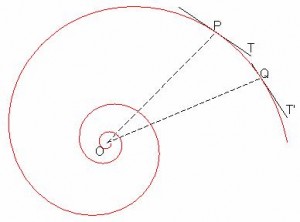Первым, кто описал ее как механическую кривую, в отличие от кривых алгебраических, был Декарт, который в 1638 г. написал монаху Мерсенну о результатах своих исследований. Декарт искал возрастающую кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке всегда один и тот же угол. Отсюда и название равноугольная. Он также показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов. Отсюда и второе название: логарифмическая спираль. Расстояние между витками растет с увеличением угла, т. е. радиус-вектор увеличивается экспоненциального с увеличением угла поворота. Так что третье название этой кривой – геометрическая спираль.

Отцом этой спирали, по всей справедливости, является Якоб Бернулли, который ее полностью изучил и которого она настолько заворожила, что он просил изобразить ее на его могиле на кладбище в Базеле с надписью “Eadem mutata resurgo’’ (“Измененная, я вновь воскресаю’’).
Каменотес не был хорошим математиком, и он вырезал на камне практически идеальную архимедову спираль.

Якоб Бернулли обнаружил некоторые свойства этой кривой, которые остались не замеченными
Декартом и Торричелли, в том числе тот факт, что логарифмическая спираль – единственная кривая, эволюта, эвольвента, каустика и подера которой также являются, в свою очередь, логарифмическими спиралями. Якоб Бернулли обнаружил еще одну необычную особенность,
самоподобие, которая прямо связывает эту спираль с фракталами.

Логарифмическая спираль, несомненно, является спиралью, которая наиболее часто встречается в природе. Царство животных предоставляет нам примеры спиралей раковин улиток и моллюсков. Все эти формы указывают на природное явление: процесс накручивания связан с процессом роста. В самом деле, раковина улитки – это не больше, не меньше, чем конус, накрученный на себя. Рога жвачных животных тоже, но они к тому же витые. И хотя физические законы роста у разных видов различны, математические законы, которые управляют ими, одинаковы: все они имеют в основе геометрическую спираль, самоподобную кривую. Если мы внимательно посмотрим на рост раковин и рогов, то заметим еще одно любопытное свойство: рост происходит только на одном конце. И это свойство сохраняет форму полностью уникальную среди кривых в математике, форму логарифмической, или равноугольной спирали.

Галактики, штормы и ураганы дают впечатляющие примеры логарифмических спиралей. И наконец, в любом месте, где есть природное явление, в котором сочетаются расширение или сжатие с вращением, поневоле появляется логарифмическая спираль. В растительном мире примеры еще более бросаются в глаза, потому что у растения может быть бесконечное число спиралей, а не только одна спираль у каждого. Расположение семечек в любом подсолнечнике, чешуек в любом ананасе, да и другие разнообразные виды растений, простые ромашки… дают нам настоящий парад переплетающихся спиралей. Если мы посмотрим сверху на любую сосновую шишку, увидим, что ее семена располагаются в виде большого числа спиралей. И это неслучайно. Это не совпадение. Семена расположены оптимально, т. е. максимально используют пространство, и эта оптимизация пространства достигается за счет расположения по спирали.
http://platea.pntic.mec.es/aperez4/curvashistoria.pdf